Unit Testing Challenge

Overview

Teaching: 10 min
Exercises: 50 min

Questions

• How do I apply unit tests to research code?

• How can I use unit tests to improve my code?

Objectives

• Use unit tests to fix some incorrectly-implemented scientific code

• Refactor code to make it easier to test

Introduction to your challenge

You have inherited some buggy code from a previous member of your research group: it has a unit test but it is currently failing. Your job is to refactor the code and write some extra tests in order to identify the problem, fix the code and make it more robust.

The code solves the heat equation, also known as the “Hello World” of Scientific Computing. It models transient heat conduction in a metal rod i.e. it describes the temperature at a distance from one end of the rod at a given time, according to some initial and boundary temperatures and the thermal diffusivity of the material:

The function heat() in diffusion.py attempts to implement a step-wise numerical approximation via a finite difference method:

This relates the temperature u at a specific location i and time point t to the temperature at the previous time point and neighbouring locations. r is defined as follows, where α is the thermal diffusivity:

We approach this problem by representing u as a Python list. Elements within the list correspond to positions along the rod, i=0 is the first element, i=1 is the second and so on. In order to increment t we update u in a loop. Each iteration, according to the finite difference equation above, we calculate values for the new elements of u.

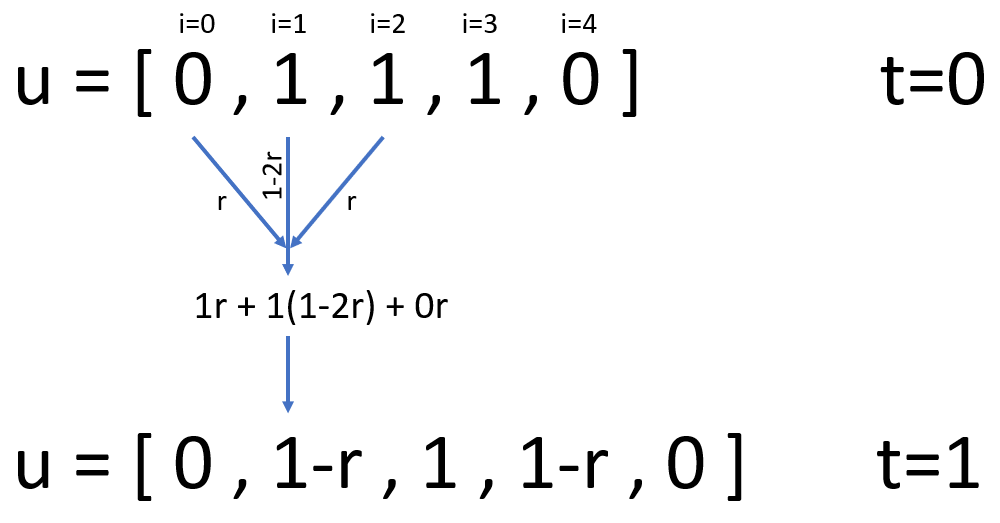
The test_heat() function in test_diffusion.py compares this approximation with the exact (analytical) solution for the boundary conditions (i.e. the temperature of the end being fixed at zero). The test is correct but failing - indicating that there is a bug in the code.

Testing (and fixing!) the code (50 min)

Work by yourself or with a partner on these test-driven development tasks. Don’t hesitate to ask a demonstrator if you get stuck!

Separation of concerns

First we’ll refactor the code, increasing its modularity. We’ll extract the code that performs a single time step into a new function that can be verified in isolation via a new unit test:

1. In diffusion.py move the logic that updates u within the loop in the heat() function to a new top-level function:

   def step(u, dx, dt, alpha):
       …
   

   Hint: the loop in heat() should now look like this:

   for _ in range(nt - 1):
       u = step(u, dx, dt, alpha)
   

2. Run the existing test to ensure that it executes without any Python errors. It should still fail.

3. Add a test for our new step() function:

   def test_step():
       assert step(…) == …
   

   It should call step() with suitable values for u (the temperatures at time t), dx, dt and alpha. It should assert that the resulting temperatures (i.e. at time t+1) match those suggested by the equation above. Use approx if necessary. _Hint: step([0, 1, 1, 0], 0.04, 0.02, 0.01) is a suitable invocation. These values will give r=0.125. It will return a list of the form [0, ?, ?, 0]. You’ll need to calculate the missing values manually using the equation in order to compare the expected and actual values.

4. Assuming that this test fails, fix it by changing the code in the step() function to match the equation - correcting the original bug. Once you’ve done this all the tests should pass.

Solution 1

Your test should look something like this:

# test_diffusion.py
def test_step():
    assert step([0, 1, 1, 0], 0.04, 0.02, 0.01) == [0, 0.875, 0.875, 0]

Your final (fixed!) step() function should look like this. The original error was a result of some over-zealous copy-and-pasting.

# diffusion.py
def step(u, dx, dt, alpha):
    r = alpha * dt / dx ** 2

    return (
        u[:1]
        + [
            r * u[i + 1] + (1 - 2 * r) * u[i] + r * u[i - 1]
            for i in range(1, len(u) - 1)
        ]
        + u[-1:]
    )

Now we’ll add some further tests to ensure the code is more suitable for publication.

Testing for exceptions

We want the step() function to raise an Exception when the following stability condition isn’t met: Add a new test test_step_unstable, similar to test_step but that invokes step with an alpha equal to 0.1 and expects an Exception to be raised. Check that this test fails before making it pass by modifying diffusion.py to raise an Exception appropriately.

Solution 2

# test_diffusion.py
def test_step_unstable():
    with pytest.raises(Exception):
        step([0, 1, 1, 0], 0.04, 0.02, 0.1)

# diffusion.py
def step(u, dx, dt, alpha):
    r = alpha * dt / dx ** 2

    if r > 0.5:
        raise Exception

    …

Adding parametrisation

Parametrise test_heat() to ensure the approximation is valid for some other combinations of L and tmax (ensuring that the stability condition remains true).

Solution 3

# test_diffusion.py
@pytest.mark.parametrize("L,tmax", [(1, 0.5), (2, 0.5), (1, 1)])
def test_heat(L, tmax):
    nt = 10
    nx = 20
    alpha = 0.01

    …

After completing these two steps check the coverage of your tests via the Test Output panel - it should be 100%.

The full, final versions of diffusion.py and test_diffusion.py are available on GitHub.

Bonus tasks

• Write a doctest-compatible docstring for step() or heat()
• Write at least one test for our currently untested linspace() function
  • Hint: you may find inspiration in numpy’s test cases, but bear in mind that its version of linspace is more capable than ours.

Key Points

• Writing unit tests can reveal issues with code that otherwise appears to run correctly

• Adding unit tests can improve software structure: isolating logical distinct code for testing often involves untangling complex structures

• pytest can be used to add simple tests for python code but also be leveraged for more complex uses like parametrising tests and adding tests to docstrings