Analysing GITT data#
PyProBE includes built-in analysis methods for pulsing experiments, which this example will demonstrate.
First import the required libraries and data:
[1]:
%%capture
%pip install matplotlib
[2]:
import matplotlib.pyplot as plt
import pyprobe
%matplotlib inline
[3]:
info_dictionary = {
"Name": "Sample cell",
"Chemistry": "NMC622",
"Nominal Capacity [Ah]": 0.04,
"Cycler number": 1,
"Channel number": 1,
}
data_directory = "../../../tests/sample_data/neware"
# Create a cell object
cell = pyprobe.Cell(info=info_dictionary)
cell.add_procedure(
procedure_name="Sample",
folder_path=data_directory,
filename="sample_data_neware.parquet",
)
print(cell.procedure["Sample"].experiment_names)
['Initial Charge', 'Break-in Cycles', 'Discharge Pulses']
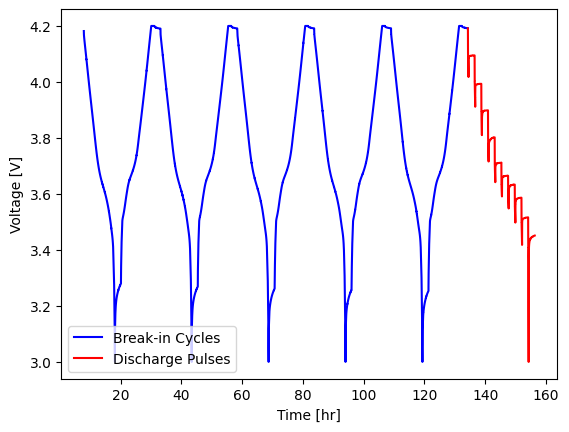
We will plot the Break-in Cycles and Discharge Pulses:
[4]:
fig, ax = plt.subplots()
cell.procedure["Sample"].experiment("Break-in Cycles").plot(
x="Time [hr]", y="Voltage [V]", ax=ax, label="Break-in Cycles", color="blue"
)
cell.procedure["Sample"].experiment("Discharge Pulses").plot(
x="Time [hr]", y="Voltage [V]", ax=ax, label="Discharge Pulses", color="red"
)
ax.set_ylabel("Voltage [V]")
[4]:
Text(0, 0.5, 'Voltage [V]')
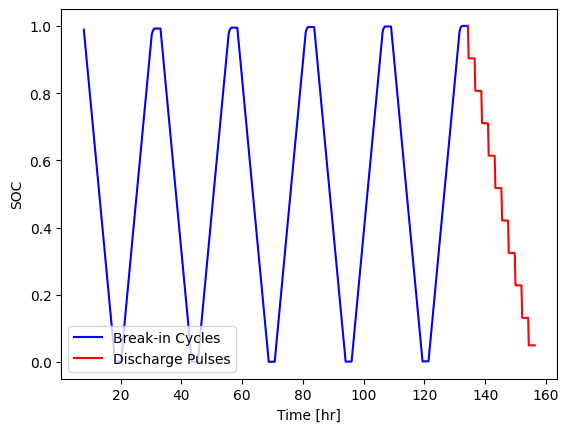
State-of-charge is a useful metric when working with battery data, however it must be carefully defined. PyProBE doesn’t automatically calculate a value for cell SOC until instructed to by the user for this reason.
To add an SOC column to the data, we call set_SOC() on the procedure. We are going to provide an argument to reference_charge. This will be the final charge of the break-in cycles. This argument instructs PyProBE that the final data point of this charge is our 100% SOC reference.
[5]:
reference_charge = cell.procedure["Sample"].experiment("Break-in Cycles").charge(-1)
cell.procedure["Sample"].set_SOC(reference_charge=reference_charge)
fig, ax = plt.subplots()
cell.procedure["Sample"].experiment("Break-in Cycles").plot(
x="Time [hr]", y="SOC", ax=ax, label="Break-in Cycles", color="blue"
)
cell.procedure["Sample"].experiment("Discharge Pulses").plot(
x="Time [hr]", y="SOC", ax=ax, label="Discharge Pulses", color="red"
)
ax.set_ylabel("SOC")
plt.legend(loc="lower left")
[5]:
<matplotlib.legend.Legend at 0x7f9291e3fb90>
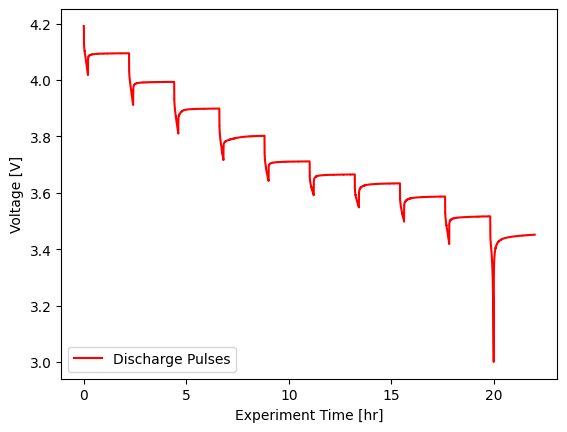
Then we’ll filter to only the pulsing experiment:
[6]:
pulsing_experiment = cell.procedure["Sample"].experiment("Discharge Pulses")
fig, ax = plt.subplots()
pulsing_experiment.plot(
x="Experiment Time [hr]",
y="Voltage [V]",
ax=ax,
label="Discharge Pulses",
color="red",
)
ax.set_ylabel("Voltage [V]")
plt.legend(loc="lower left")
[6]:
<matplotlib.legend.Legend at 0x7f92919a0170>
And then create our pulsing analysis object.
[7]:
from pyprobe.analysis import pulsing
pulse_object = pulsing.Pulsing(input_data=pulsing_experiment)
With the pulsing object we can separate out individual pulses:
[8]:
fig, ax = plt.subplots()
pulse_object.input_data.plot(
x="Experiment Time [hr]",
y="Voltage [V]",
label="Full Experiment",
color="blue",
ax=ax,
)
pulse_object.pulse(4).plot(
x="Experiment Time [hr]", y="Voltage [V]", label="Pulse 5", color="red", ax=ax
)
ax.set_ylabel("Voltage [V]")
[8]:
Text(0, 0.5, 'Voltage [V]')
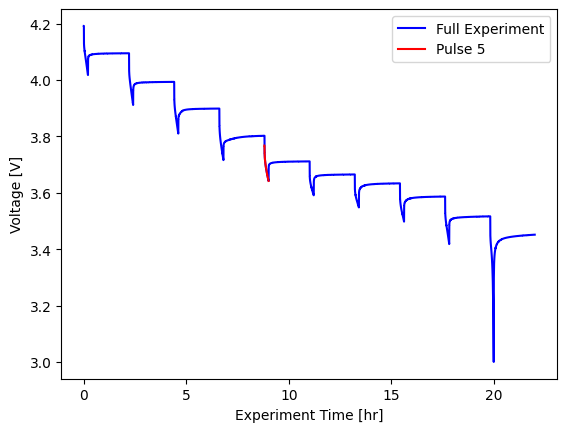
We can also extract key parameters from the pulsing experiment, with the get_resistances() method.
[9]:
pulse_resistances = pulsing.get_resistances(input_data=pulsing_experiment)
print(pulse_resistances.data)
shape: (10, 5)
┌──────────┬──────────────┬─────────┬───────────────┬───────────┐
│ SOC ┆ Pulse Number ┆ OCV [V] ┆ Capacity [Ah] ┆ R0 [Ohms] │
│ --- ┆ --- ┆ --- ┆ --- ┆ --- │
│ f64 ┆ u32 ┆ f64 ┆ f64 ┆ f64 │
╞══════════╪══════════════╪═════════╪═══════════════╪═══════════╡
│ 1.0 ┆ 1 ┆ 4.1919 ┆ 0.062214 ┆ 1.805578 │
│ 0.903497 ┆ 2 ┆ 4.0949 ┆ 0.058214 ┆ 1.835632 │
│ 0.806994 ┆ 3 ┆ 3.9934 ┆ 0.054213 ┆ 1.775612 │
│ 0.710493 ┆ 4 ┆ 3.8987 ┆ 0.050213 ┆ 1.750596 │
│ 0.613991 ┆ 5 ┆ 3.8022 ┆ 0.046213 ┆ 1.725532 │
│ 0.517489 ┆ 6 ┆ 3.7114 ┆ 0.042212 ┆ 1.705558 │
│ 0.420988 ┆ 7 ┆ 3.665 ┆ 0.038212 ┆ 1.705622 │
│ 0.324487 ┆ 8 ┆ 3.6334 ┆ 0.034212 ┆ 1.735555 │
│ 0.227986 ┆ 9 ┆ 3.5866 ┆ 0.030212 ┆ 1.795638 │
│ 0.131485 ┆ 10 ┆ 3.5164 ┆ 0.026211 ┆ 1.900663 │
└──────────┴──────────────┴─────────┴───────────────┴───────────┘
The get_resistances() method can take an argument of a list of times at which to evaluate the resistance after the pulse, for instance at 10s after the pulse:
[10]:
pulse_resistances = pulsing.get_resistances(input_data=pulsing_experiment, r_times=[10])
print(pulse_resistances.data)
shape: (10, 6)
┌──────────┬──────────────┬──────────────┬─────────┬───────────────┬───────────┐
│ SOC ┆ Pulse Number ┆ R_10s [Ohms] ┆ OCV [V] ┆ Capacity [Ah] ┆ R0 [Ohms] │
│ --- ┆ --- ┆ --- ┆ --- ┆ --- ┆ --- │
│ f64 ┆ u32 ┆ f64 ┆ f64 ┆ f64 ┆ f64 │
╞══════════╪══════════════╪══════════════╪═════════╪═══════════════╪═══════════╡
│ 1.0 ┆ 1 ┆ 2.910931 ┆ 4.1919 ┆ 0.062214 ┆ 1.805578 │
│ 0.903497 ┆ 2 ┆ 2.805967 ┆ 4.0949 ┆ 0.058214 ┆ 1.835632 │
│ 0.806994 ┆ 3 ┆ 2.735943 ┆ 3.9934 ┆ 0.054213 ┆ 1.775612 │
│ 0.710493 ┆ 4 ┆ 2.685915 ┆ 3.8987 ┆ 0.050213 ┆ 1.750596 │
│ 0.613991 ┆ 5 ┆ 2.640815 ┆ 3.8022 ┆ 0.046213 ┆ 1.725532 │
│ 0.517489 ┆ 6 ┆ 2.400785 ┆ 3.7114 ┆ 0.042212 ┆ 1.705558 │
│ 0.420988 ┆ 7 ┆ 2.345855 ┆ 3.665 ┆ 0.038212 ┆ 1.705622 │
│ 0.324487 ┆ 8 ┆ 2.390765 ┆ 3.6334 ┆ 0.034212 ┆ 1.735555 │
│ 0.227986 ┆ 9 ┆ 2.565912 ┆ 3.5866 ┆ 0.030212 ┆ 1.795638 │
│ 0.131485 ┆ 10 ┆ 3.026056 ┆ 3.5164 ┆ 0.026211 ┆ 1.900663 │
└──────────┴──────────────┴──────────────┴─────────┴───────────────┴───────────┘
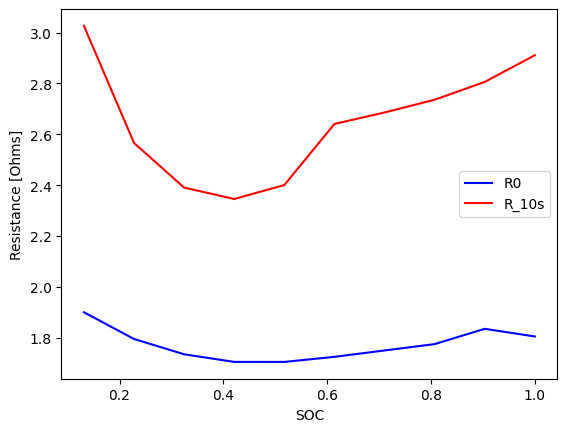
As a result object, the pulse summary can also be plotted:
[11]:
fig, ax = plt.subplots()
pulse_resistances.plot(x="SOC", y="R0 [Ohms]", ax=ax, label="R0", color="blue")
pulse_resistances.plot(x="SOC", y="R_10s [Ohms]", ax=ax, label="R_10s", color="red")
ax.set_ylabel("Resistance [Ohms]")
[11]:
Text(0, 0.5, 'Resistance [Ohms]')