shape_functions_linear_quadratic Module Reference

Shape function subroutines for multi-dimensions for Quadrilaterals, Triangles, Hexaedra and Tetrahedra. More...

Data Types
interface	detnlxr
	: Calculates the derivatives of the shape functions More...
interface	detnlxr_invjac
	: Computes the derivatives of the shape functions and the inverse of the Jacobian More...

Functions/Subroutines
subroutine	re2dn4 (lowqua, ngi, ngi_l, nloc, mloc, m, weight, n, nlx, nly, sngi, snloc, sweigh, sn, snlx, l1, l2)
	at the Gauss points. NB: We may need to define surface elements for p and (u,v,w) More...
subroutine	re3dn8 (lowqua, ngi, ngi_l, nloc, mloc, m, weight, n, nlx, nly, nlz, sngi, snloc, sweigh, sn, snlx, snly, l1, l2, l3)
	This subrt. computes the shape functions M and N and their derivatives at the Gauss points for 3D. If LOWQUA, then use one point quadrature else use 8 point quadrature. NB.: LX/YP(I) are the local X/Y coordinates of nodal point I. More...
subroutine	re2dn9 (lowqua, ngi, ngi_l, nloc, mloc, m, weight, n, nlx, nly, l1, l2)
	Quadratic variation (2D) for velocity – 9 node brick element. Linear variation (2D) for pressure – 4 node brick element. NB.: We may need to define surface elements for p and (u,v,w). More...
subroutine	re3d27 (lowqua, ngi, ngi_l, nloc, mloc, m, weight, n, nlx, nly, nlz, l1, l2, l3)
	Quadratic variation (3D) for velocity – 27 node brick element. Linear variation (3D) for pressure – 8 node brick element. NB.: We may need to define surface elements for p and (u,v,w). More...
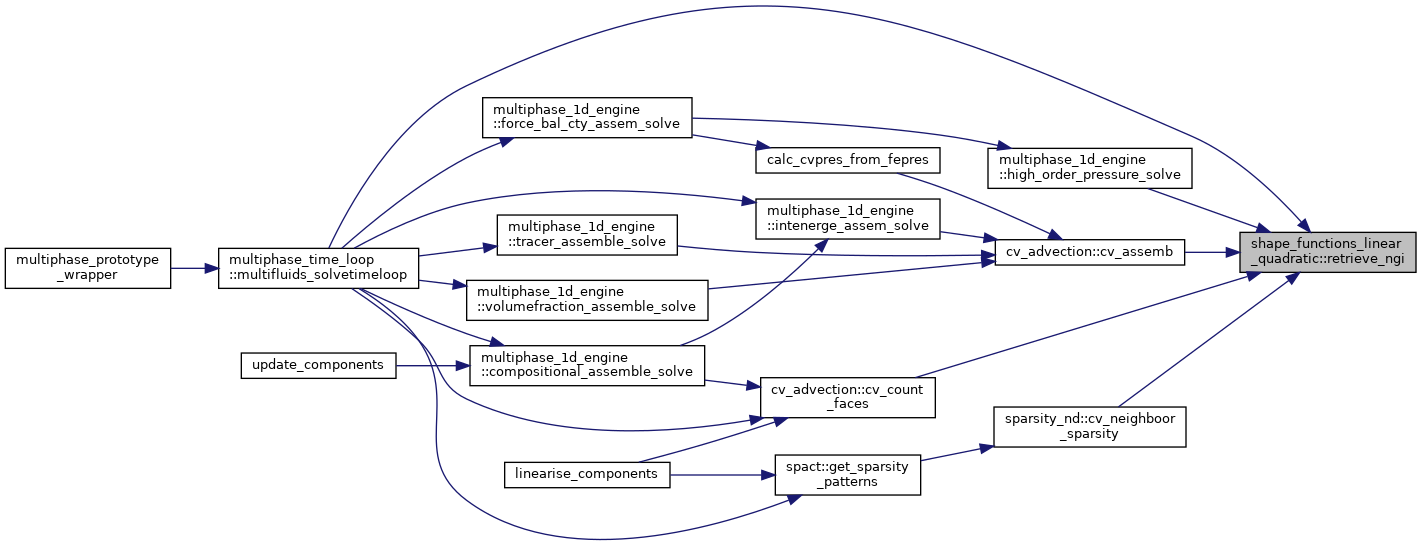
subroutine	retrieve_ngi_old (ndim, cv_ele_type, cv_nloc, u_nloc, cv_ngi, cv_ngi_short, scvngi, sbcvngi, nface, QUAD_OVER_WHOLE_ELE)
	Obtains the gauss integration numbers given the input parameters use retrieve_ngi instead of this one since it uses data types retrieve_ngi. More...
subroutine	retrieve_ngi (GIdims, Mdims, cv_ele_type, QUAD_OVER_WHOLE_ELE, scalar_nloc, vector_nloc)
	: Computes the number of Gauss integration points and all the necessary information More...
subroutine	lagrot (weit, quadpos, ndgi, getndp)
	This computes the weight and points for standard Gaussian quadrature. If (GETNDP == T) then get the position of the nodes and neglect the weights. More...
real function	lagran (diff, lx, inod, ndnod, nodpos)
	This return the Lagrange poly assocaited with node INOD at point LX If DIFF then send back the value of this poly differentiated. More...
real function	rgptwe (IG, ND, WEIGHT)
	If WEIGHT is TRUE in function RGPTWE then return the Gauss-pt weight else return the Gauss-pt. There are ND Gauss points – we are looking for either the weight or the x-coord of the IG'th Gauss point. More...
subroutine	quad_basis_funs_1d (sngi, snloc, sweigh, sn, snlx)
	determine the 1d shape functions sn and its local derivative slnx. More...

Variables
logical	new_high_order_vol_quadratic_ele_quadrature = .false.
logical	new_quadratic_ele_quadrature = .false.

Detailed Description

Shape function subroutines for multi-dimensions for Quadrilaterals, Triangles, Hexaedra and Tetrahedra.

Function/Subroutine Documentation

lagran()

real function shape_functions_linear_quadratic::lagran	(	logical	diff,
		real	lx,
		integer	inod,
		integer	ndnod,
		real, dimension( 0 : ndnod - 1 )	nodpos
	)

This return the Lagrange poly assocaited with node INOD at point LX If DIFF then send back the value of this poly differentiated.

Here is the caller graph for this function:

lagrot()

subroutine shape_functions_linear_quadratic::lagrot	(	real, dimension( : ), intent(inout)	weit,
		real, dimension( : ), intent(inout)	quadpos,
		integer, intent(in)	ndgi,
		logical, intent(in)	getndp
	)

This computes the weight and points for standard Gaussian quadrature. If (GETNDP == T) then get the position of the nodes and neglect the weights.

Here is the call graph for this function:

Here is the caller graph for this function:

quad_basis_funs_1d()

subroutine shape_functions_linear_quadratic::quad_basis_funs_1d	(	integer, intent(in)	sngi,
		integer, intent(in)	snloc,
		real, dimension( : ), intent(inout)	sweigh,
		real, dimension( :, : ), intent(inout)	sn,
		real, dimension( :, : ), intent(inout)	snlx
	)

determine the 1d shape functions sn and its local derivative slnx.

Here is the call graph for this function:

Here is the caller graph for this function:

re2dn4()

subroutine shape_functions_linear_quadratic::re2dn4	(	logical, intent(in)	lowqua,
		integer, intent(in)	ngi,
		integer, intent(in)	ngi_l,
		integer, intent(in)	nloc,
		integer, intent(in)	mloc,
		real, dimension( :, : ), intent(inout)	m,
		real, dimension( : ), intent(inout)	weight,
		real, dimension( :, : ), intent(inout)	n,
		real, dimension( :, : ), intent(inout)	nlx,
		real, dimension( :, : ), intent(inout)	nly,
		integer, intent(in)	sngi,
		integer, intent(in)	snloc,
		real, dimension( : ), intent(inout)	sweigh,
		real, dimension( :, : ), intent(inout)	sn,
		real, dimension( :, : ), intent(inout)	snlx,
		real, dimension(: ), intent(in)	l1,
		real, dimension(: ), intent(in)	l2
	)

at the Gauss points. NB: We may need to define surface elements for p and (u,v,w)

Here is the call graph for this function:

Here is the caller graph for this function:

re2dn9()

subroutine shape_functions_linear_quadratic::re2dn9	(	logical, intent(in)	lowqua,
		integer, intent(in)	ngi,
		integer, intent(in)	ngi_l,
		integer, intent(in)	nloc,
		integer, intent(in)	mloc,
		real, dimension( :, : ), intent(inout)	m,
		real, dimension( : ), intent(inout)	weight,
		real, dimension( :, : ), intent(inout)	n,
		real, dimension( :, : ), intent(inout)	nlx,
		real, dimension( :, : ), intent(inout)	nly,
		real, dimension( : ), intent(in)	l1,
		real, dimension( : ), intent(in)	l2
	)

Quadratic variation (2D) for velocity – 9 node brick element. Linear variation (2D) for pressure – 4 node brick element. NB.: We may need to define surface elements for p and (u,v,w).

This is for the 2-D 27node element, which is number as follows | /Z Y| / |/ +----—X For Z = -1 ... 7 8 9 4 5 6 1 2 3 For M the shape functions have local node numbers For Z = -1 ... 4 3

1 2

Here is the caller graph for this function:

re3d27()

subroutine shape_functions_linear_quadratic::re3d27	(	logical, intent(in)	lowqua,
		integer, intent(in)	ngi,
		integer, intent(in)	ngi_l,
		integer, intent(in)	nloc,
		integer, intent(in)	mloc,
		real, dimension( :, : ), intent(inout)	m,
		real, dimension( : ), intent(inout)	weight,
		real, dimension( :, : ), intent(inout)	n,
		real, dimension( :, : ), intent(inout)	nlx,
		real, dimension( :, : ), intent(inout)	nly,
		real, dimension( :, : ), intent(inout)	nlz,
		real, dimension( : ), intent(in)	l1,
		real, dimension( : ), intent(in)	l2,
		real, dimension( : ), intent(in)	l3
	)

Quadratic variation (3D) for velocity – 27 node brick element. Linear variation (3D) for pressure – 8 node brick element. NB.: We may need to define surface elements for p and (u,v,w).

This is for the 2-D 27node element, which is number as follows | /Z Y| / |/ +----—X For Z = -1 ... 7 8 9 4 5 6 1 2 3 For Z = 0 ... 16 17 18 13 14 15 10 11 12 For Z = 1 ... 25 26 27 22 23 24 19 20 21 For M the shape functions have local node numbers For Z = -1 ... 4 3

1 2 For Z = 1 ... 8 7

5 6

Here is the caller graph for this function:

re3dn8()

subroutine shape_functions_linear_quadratic::re3dn8	(	logical, intent(in)	lowqua,
		integer, intent(in)	ngi,
		integer, intent(in)	ngi_l,
		integer, intent(in)	nloc,
		integer, intent(in)	mloc,
		real, dimension( :, : ), intent(inout)	m,
		real, dimension( : ), intent(inout)	weight,
		real, dimension( :, : ), intent(inout)	n,
		real, dimension( :, : ), intent(inout)	nlx,
		real, dimension( :, : ), intent(inout)	nly,
		real, dimension( :, : ), intent(inout)	nlz,
		integer, intent(in)	sngi,
		integer, intent(in)	snloc,
		real, dimension( : ), intent(inout)	sweigh,
		real, dimension( :, : ), intent(inout)	sn,
		real, dimension( :, : ), intent(inout)	snlx,
		real, dimension( :, : ), intent(inout)	snly,
		real, dimension( : ), intent(in)	l1,
		real, dimension( : ), intent(in)	l2,
		real, dimension( : ), intent(in)	l3
	)

This subrt. computes the shape functions M and N and their derivatives at the Gauss points for 3D. If LOWQUA, then use one point quadrature else use 8 point quadrature. NB.: LX/YP(I) are the local X/Y coordinates of nodal point I.

Here is the call graph for this function:

Here is the caller graph for this function:

retrieve_ngi()

subroutine shape_functions_linear_quadratic::retrieve_ngi	(	type( multi_gi_dimensions ), intent(inout)	GIdims,
		type( multi_dimensions ), intent(in)	Mdims,
		integer, intent(in)	cv_ele_type,
		logical, intent(in)	QUAD_OVER_WHOLE_ELE,
		integer, intent(in), optional	scalar_nloc,
		integer, intent(in), optional	vector_nloc
	)

: Computes the number of Gauss integration points and all the necessary information

Parameters

GIdims	output Gauss integration numbers
Mdims	dimensions of the domain
cv_ele_type	type of element, 1D, 2D, 3D, triangle, tetrahedron etc...
QUAD_OVER_WHOLE_ELE	if QUAD_OVER_WHOLE_ELE=.true. then dont divide element into CV's to form quadrature.
scalar_nloc	if present then overwrite the cv_nloc given by Mdims
vector_nloc	if present then overwrite the u_nloc given by Mdims

Here is the caller graph for this function:

retrieve_ngi_old()

subroutine shape_functions_linear_quadratic::retrieve_ngi_old	(	integer, intent(in)	ndim,
		integer, intent(in)	cv_ele_type,
		integer, intent(in)	cv_nloc,
		integer, intent(in)	u_nloc,
		integer, intent(inout)	cv_ngi,
		integer, intent(inout)	cv_ngi_short,
		integer, intent(inout)	scvngi,
		integer, intent(inout)	sbcvngi,
		integer, intent(inout)	nface,
		logical, intent(in)	QUAD_OVER_WHOLE_ELE
	)

Obtains the gauss integration numbers given the input parameters use retrieve_ngi instead of this one since it uses data types retrieve_ngi.

rgptwe()

real function shape_functions_linear_quadratic::rgptwe	(	integer	IG,
		integer	ND,
		logical	WEIGHT
	)

If WEIGHT is TRUE in function RGPTWE then return the Gauss-pt weight else return the Gauss-pt. There are ND Gauss points – we are looking for either the weight or the x-coord of the IG'th Gauss point.

Here is the caller graph for this function:

Variable Documentation

new_high_order_vol_quadratic_ele_quadrature

logical shape_functions_linear_quadratic::new_high_order_vol_quadratic_ele_quadrature = .false.

new_quadratic_ele_quadrature

logical shape_functions_linear_quadratic::new_quadratic_ele_quadrature = .false.