Using CNNs to learn about the physics of the birth of the first stars in the Universe¶
A brief History of the Universe ¶
The history of the Universe can be split into several phases. It 'started'1 with the big bang, followed by the period of cosmic inflation. This created fundamental particles, and from the resulting asymmetry between matter and antimatter, the quark-gluon plasma formed. As the primordial quark-gluon plasma cooled, protons and neutrons formed. The energy released from baryon formation and other processes led to an abundance of photons at this time. This period is known the radiation dominated era.
As the Universe cooled even more, it transitioned into the matter dominated era, at $z \approx 3300$. At $z \approx 1100$ (100 000 years after the Big Bang), the Universe was cool enough for electrons to recombine with protons to form neutral hydrogen -- which then combined to form the lighter elements (known as recombination). This led to photons' decoupling from baryons, creating what we now observe as the Cosmic Microwave Background (CMB).
Following the formation of the CMB, the Universe went through what's known as the dark ages; this is when the Universe was made primarily of neutral gasses, and no stars. As the universe cooled even more, these neutral gasses started to collapse and create the first stars and galaxies. These first stars (called population III stars) flooded the surrounding gas with ionising photons. This period in the Universe's history is known as the Epoch of Reionisation (EoR). As more stars and galaxies formed, the entire inter-stellar medium became ionised again. The evolution of the Universe's history is shown in the sketch below:
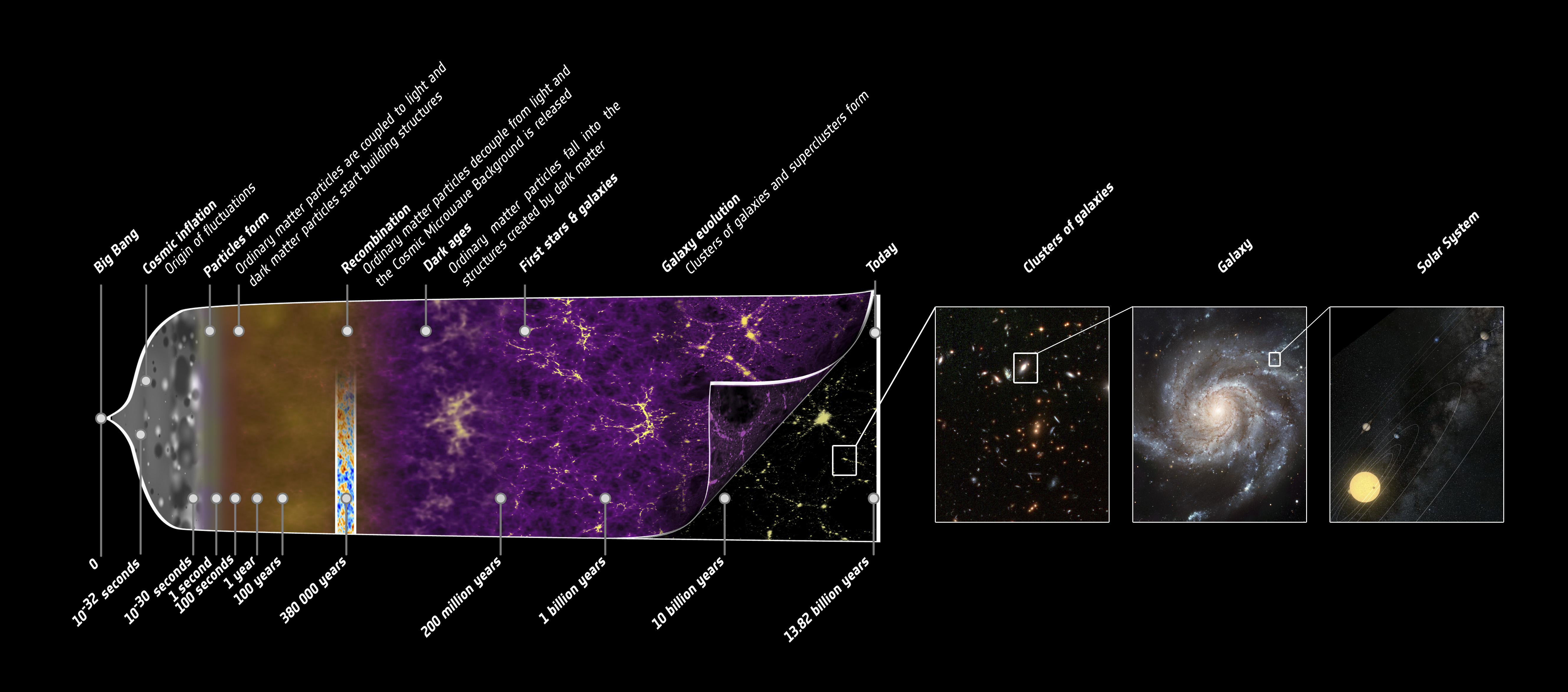
1 Using 'started' in a very loose sense.
Setting up the problem ¶
An open problem in EoR research is how best to constrain the reionization history using 21 cm intensity measurements. One common approach is to use summary statistics such as the power spectrum2. Fully Bayesian parameter inference methods have been developed for this task3. However, the 21~cm signal from the EoR is expected to be non-Gaussian, implying that there is significant information encoded in higher-order statistics such as the bispectrum4. But all such summaries still entail some loss of information. The Square Kilometer Array(SKA)5 will produce tomography throughout the EoR, allowing the possibility of inferring parameters from the maps themselves. However, the amount of data and large parameter space pose significant challenges for traditional statistical inference methods, and instead the problem necessitates the deployment of machine learning methods.
2 Trotta et al (2016), Pober et al (2014)
3 Greig et al (2015), Greig et al (2017)
4 Majumdar et al (2018), Shimabukuro et al (2016)
5 www.skao.int
The SKA will only come online at the end of the decade, hence the this tomographical data does not exist yet. In order to prepare for the deluge of data that will come from this next generation telescope, we need to create mock data to train machine learning models and create data analysis pipelines. One method to create this mock data is to use semi-numerical simulations. In this tutorial we will be using SimFast21 6. Okay but what are we actually simulating? Well, the SKA will be observing the 21 cm emmision line that comes from neutral hydrogen and hence it will be able to probe the hydrogen gas clouds during the EoR. The general idea is that when the first stars and galaxies were formed, they started to ionise the surrounding gas. So what we should see is small bubbles of ionised gas start to form around the stars and galaxies. As time goes on, these bubbles will grow and start to overlap, eventually leading to all the hydrogen in the universe becoming ionised. An example simulation is shown below:

By studying how these bubbles form, change and grow we can infer a lot about the underlying physics that drives it. One of the easiest measurements one can make is called the ionisation fraction($x_{HI} $), This is the fraction of ionised hydrogen present in a volume. This is the parameter we will be attempting to infer from our simulations.
Okay, so with all that background out of the way, we can finally get back to some machine learning. The first thing we will need is some data. You're welcome to clone the SimFast21 github page7 and simulate the data we will be using for yourself, however if this sounds too intimidating at the moment then we can just download a pre-simulated dataset here.
6 Santos et al (2008), Hassan et al (2016)
Exploring the dataset ¶
Before we can do any exploring, we need to read in the dataset. Handily, this dataset was pickled with pandas so will be really easy to load. Let's import pandas and any other packages that may come in handy.
import pandas as pd
import numpy as np
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3' #turns off tensorflow warnings
import tensorflow as tf
#pretty plots
import pylab as pl
import seaborn as sns
sns.set(style="ticks")
color_palette = sns.color_palette("Set3",5)[::-1]
sns.set_palette(color_palette)
#Download dataset
#Dataset was too large for git, so using a google drive link instead.
!wget --load-cookies /tmp/cookies.txt "https://drive.google.com/uc?export=download&confirm=$(wget --quiet --save-cookies /tmp/cookies.txt --keep-session-cookies --no-check-certificate 'https://drive.google.com/uc?export=download&id=17nmV0nSkDauSnHnm78xuUDUrCR8p2ldp' -O- | sed -rn 's/.*confirm=([0-9A-Za-z_]+).*/\1\n/p')&id=17nmV0nSkDauSnHnm78xuUDUrCR8p2ldp" -O 'df_recode.gzip' && rm -rf /tmp/cookies.txt
df_dataset = pd.read_pickle("df_recode.gzip",compression={'method': 'gzip', 'compresslevel': 1, 'mtime': 1})
Now we can use pandas to explore the dataset:
df_dataset.head() #prints first five entries of pandas dataframe
We can see that there are five columns. The first column, named maps contain the images (2d maps) that we will be using to train the network. For now, we will just be using the column called xHI as the labels. The other column that will prove to be useful in a few minutes is the redshift column. We will return to the other parameters at a later stage, so for now, let's create a new dataframe with just the columns we need:
df_dataset = df_dataset[['maps','xHI','redshift']]
df_dataset.head()
In the same way as before, we can have a look at the shapes of our data to get some insight into what they are.
print('--------- dataset -----------')
print('x Shape: ', df_dataset['maps'].values.shape )
print('y Shape: ', df_dataset['xHI'].values.shape )
We expected xHI to be a 1D array, however, maps is not quite what we expected. We expected these to be 2D images, but we got a 1D array, let's see what's happening here.
print(df_dataset['maps'].values[0])
print('Shape: ', df_dataset['maps'].values[0].shape )
Okay, so we see that if we look at one map from our dataset, it is indeed a 2D image. This means that df_dataset['maps'].values returned a list of all the 2D maps and hence once a one 1D array. Before we fix that, let's split the dataset into a training and test set. To this is we will use the inbuilt function from scikit-learn8
8 https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html
from sklearn.model_selection import train_test_split
#test set size will be 20% of the full dataset
df_train, df_test = train_test_split(df_dataset, test_size=.2, shuffle=True, random_state=42)
As with all datasets with machine learning, we need to first do some pre-processing before we can do any training. This is a crucial step in the ML process. Biases in the training set can lead to wildly incorrect results from the network. I can not stress enough how important it is to correctly pre-process your dataset. You need to think carefully about what you are trying to infer with the network and all the ways in which the network can misinterpret this because of biases in the training set.
Right, so let's see if we can think of different types of biases we could have in our dataset. The first would require some insight of the physics involved in our simulation so I will give this to you for free.
Recall that the parameter we are trying to infer is $ x_{HI} $, which can be thought of a measure of the number and sizes of bubbles in our images. Let's think about what a really high or really low $ x_{HI} $ would mean for the bubbles in our images. A really low $ x_{HI} $ would mean no or very few small ionsied bubbles. A really high $ x_{HI} $ would mean most if not all of the image would be covered with overlapping bubbles. Visually, both these images would look very similiar while having completely different $ x_{HI} $ values. This would be incredibly hard for our network to different between and hence would bias the results. To mitigate this we will remove all images with really high or really low $ x_{HI} $ from our dataset9.
9 Remember that everything you do to the training set must also be done to the test set.
df_train = df_train.drop(df_train[df_train['xHI'] > 0.99].index)
df_train = df_train.drop(df_train[df_train['xHI'] < 0.01].index)
df_test = df_test.drop(df_test[df_test['xHI'] > 0.99].index)
df_test = df_test.drop(df_test[df_test['xHI'] < 0.01].index)
Now let's have a look at some statistics. We know that as time moves forward (or redshift gets smaller) the bubbles increase in size, hence $ x_{HI} $ changes. Let's plot the distribution of $ x_{HI} $ for each of the different redshifts we have.
#Extract the unique redshifts in our dataset
redshifts = df_train['redshift'].unique()
print('Redshifts:', redshifts)
df_train['xHI'].hist(by=df_train['redshift'])
Exercise 1 ¶
We can see that our data is well sampled across $ x_{HI} $, however, there are still some cases in which there is more or less images in a $ x_{HI} $ bin than the rest of the bins. Balance the dataset such that all bins across all redshifts have the same number of images in each $ x_{HI} $ bin.
####------------------------------------------------------------------####
# #
# #
# #
# #
# Add code here #
# #
# #
# #
####------------------------------------------------------------------####
Now that our dataset is balanced, we can split the dataset into images and labels, then reshape them as we mentioned earlier before doing some more pre-processing.
#output from dataset is weird list, so have to do it this way to make maps an array with correct dimensions.
train_x = np.array(list(df_train['maps'].values)).reshape(len(df_train),200,200,1)
train_y = df_train['xHI'].values
test_x = np.array(list(df_test['maps'].values)).reshape(len(df_test),200,200,1)
test_y = df_test['xHI'].values
print('---------Train data -----------')
print('x Shape: ', train_x.shape )
print('y Shape: ', train_y.shape )
print('---------Test data -----------')
print('x Shape: ', test_x.shape )
print('y Shape: ', test_y.shape )
We can now have a look at some more statistics. We can have look at the minimum and maximum pixel values in an image. We can also have a look at the mean and standard deviation across the dataset.
print('---------Train data -----------')
print('Min: ', np.min(train_x[0]))
print('Max: ', np.max(train_x[0]))
print('Mean: ', np.mean(train_x))
print('Std:', np.std(train_x))
Exercise 2 ¶
In the intro tutorial, we normalised the dataset. This time see if you can normalise and standardise our dataset. Remember that this should be done to the testing set as well.
####------------------------------------------------------------------####
# #
# #
# #
# #
# Add code here #
# #
# #
# #
####------------------------------------------------------------------####
Training the Network ¶
Now we are finally ready to do some training! First we need the VGG architecture that we introduced in the last tutorial:
def make_model_VGG(output = 1,l_rate = 0.01, loss = 'mean_squared_error',):
'''
Creates a CNN with the VGG architecture.
Params:
-------
output: int
The number of output neurons.
l_rate: float
The learning rate for the given loss function.
loss: str
Loss function to use, only excepts tf loss functions
Returns:
--------
Tensorflow sequential model.
'''
initializer = tf.keras.initializers.GlorotNormal()
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(32, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.Conv2D(32, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
model.add(tf.keras.layers.Conv2D(64, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.Conv2D(64, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
model.add(tf.keras.layers.Conv2D(128, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.Conv2D(128, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
model.add(tf.keras.layers.Conv2D(256, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.Conv2D(256, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(1024,kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.Dense(1024,kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.Dense(1024,kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.Dense(output,kernel_initializer=initializer,use_bias =False))
model.compile(loss=loss,
optimizer=tf.keras.optimizers.Adam(learning_rate = l_rate),
metrics=[tf.keras.metrics.RootMeanSquaredError()])
return model
# Create a callback that saves the model's weights
checkpoint_path = "training/cp-{epoch:04d}.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
save_weights_only=False,
verbose=1)
output_nuerons = 1
learning_rate = 0.01
batch_size = 16
model = make_model_VGG(output_nuerons,learning_rate)
history = model.fit(train_x, train_y,
batch_size=batch_size,
epochs=10,
verbose=1,
callbacks=[cp_callback])
pickle.dump(history.history['loss'], open( dirname+"loss.p", "wb" ) )
Analysing Results ¶
Now we have a trained network, this is not the end. We need to use this network to do some science! In order to do that we first need to check the performance of our network. One method to do this is to plot the label predicted by our network against the true label for each of the images in our test set. If our network is doing well, we should expect this to be a straight line. Below I have defined a small function that does this for us:
from sklearn.metrics import r2_score
def plot_results(test_x,test_y,model,save = False,plotname='plot.pdf'):
'''
Plots the results of the trained network on the test set
Params
------
test_x: array
The test image data.
test_y: array
Corresponding labels for image data.
model: tf model object
The trained model to test
save: boolean
Parameter dictating whether or not to save the output image. (Default: False)
plotname: str
Name of output image.
Returns
-------
Plot showing results.
'''
predictions = model.predict(test_x)
fig = pl.figure(figsize=(12,6))
fs = 16 #changes the font size in the plots
r2 = r2_score(test_y,predictions)
pl.plot(test_y,predictions,'.',alpha = 0.9,label = r'$R^2$= '+str(np.round(r2,3)))
line = np.linspace(np.min(test_y),np.max(test_y),100)
pl.plot(line,line,color = '#696969',linewidth = 2)
pl.locator_params(axis='x', nbins=8)
ax = pl.gca()
for tick in ax.xaxis.get_major_ticks():
tick.label.set_fontsize(fs)
for tick in ax.yaxis.get_major_ticks():
tick.label.set_fontsize(fs)
pl.xlabel('Ground Truth',fontsize = fs-1, fontweight = 'bold')
pl.ylabel('Predicted',fontsize = fs-1, fontweight = 'bold')
pl.legend(fontsize = fs-2)
sns.despine()
if save:
pl.savefig(plotname)
pl.show()
With that in hand we can have a look at the performance of the network. With this dataset and this architecture we would expect the network to do really well, so we expect a R2 score ~ 1. See how close you can get to this by using everything you have learnt so far.
trained_model = model
#---Uncomment this if you want to load a specific trained model------###
# trained_model = tf.keras.models.load_model('training/cp-0010.ckpt')
plot_results(test_x,test_y,trained_model)
Jupyter Notebooks are great for interogating datasets and prototyping code, but when you want to scale up your code to run on a local cluster or a remote cluster such as the Imperial HPC then notebooks are a bit clunky. In order to scale up the code we have written, we will need to move everything into a script file. See the notebook titled 'Converting to a python script' for more