Introduction to Convolutional Neural Networks¶
When getting into deep learning for the first time, you will hear a lot of common terms being thrown around. The first is Tensorflow and Pytorch. These are two competing deep learning frameworks. Tensorflow was created by the Google Brain team and Pytorch was developed by Meta AI. Each of these frameworks have their own set of pros and cons which we will not get into here1. For the purpose of this exemplar we will be using Tensorflow.
The second common term you will hear is Keras. Keras is an API written in python, it interfaces with many different deep learning backends and makes building models considerably easier. Thankfully, we do not need to concern ourselves with how this all works because as of Tensorflow v2, Keras has been fully integrated.
1For more on the pros and cons of each framework refer to this great blog post: https://www.v7labs.com/blog/pytorch-vs-tensorflow.
Now, with our newfound knowledge let's see if Tensorflow is installed.
import tensorflow as tf
print(tf.__version__)
2.12.0
If everything went well with setting up the virtual environment then you should see a tensorflow version >= 2.12
Next we will import some packages that may prove to be useful later on.
import numpy as np
import pylab as pl
import seaborn as sns #pretty plots
Getting started with Mnist ¶
The first thing we are going to do is fimilarise ourselves with Tensorflow. The easiest way to do this is through example. So, we will be following a small Tensorflow tutorial. The first thing we will need is some data. Luckily, tensorflow comes prepackaged with some data.
data = tf.keras.datasets.mnist.load_data()
This is the very popular Mnist dataset, which you may or may not have seen in other tutorials. It's a dataset of handwritten numbers from 0 - 9. While that is a fairly boring dataset, it will work just fine for our purposes.
The next think we need to do is explore the dataset:
print('Type: ', type(data))
print('Shape: ', len(data))
Type: <class 'tuple'> Shape: 2
We know our data is a tuple with length 2. So let's extract that into its own variables (the variable names may contain spoilers for what they are). Then repeat the steps above:
train_data, test_data = data
print('---------Train Data-----------')
print('Type: ', type(train_data))
print('Shape: ', len(train_data))
print('---------Test Data-----------')
print('Type: ', type(test_data))
print('Shape: ', len(test_data))
---------Train Data----------- Type: <class 'tuple'> Shape: 2 ---------Test Data----------- Type: <class 'tuple'> Shape: 2
Extract once more.....
x_train, y_train = train_data
x_test, y_test = test_data
print('---------Train x_data -----------')
print('Type: ', type(x_train))
print('Shape: ', len(x_train))
print('---------Train y_data -----------')
print('Type: ', type(y_train))
print('Shape: ', len(y_train))
---------Train x_data ----------- Type: <class 'numpy.ndarray'> Shape: 60000 ---------Train y_data ----------- Type: <class 'numpy.ndarray'> Shape: 60000
Now we're getting somewhere! Our data are numpy arrays. With numpy arrays we use a more informative command, instead of len(), to see what the array looks like:
print('---------Train data -----------')
print('x Shape: ', x_train.shape )
print('y Shape: ', y_train.shape )
print('---------Test data -----------')
print('x Shape: ', x_test.shape )
print('y Shape: ', y_test.shape )
---------Train data ----------- x Shape: (60000, 28, 28) y Shape: (60000,) ---------Test data ----------- x Shape: (10000, 28, 28) y Shape: (10000,)
Now we have a picture of what our data is. We can see that the training data consists of 60000 images which are 28X28 in dimension and the test data consists of 10000 with the same dimensions. We can also see the x_data contains the images and y_data contains the labels. With this, let's use more informative variable names:
train_images, train_labels = x_train, y_train
test_images, test_labels = x_test, y_test
Exploring the dataset ¶
Now let's have a look at one of the images with the corresponding label:
###------------------------------------------------------------------------####
# Hands on 1 #
# ------------ #
# Change image_idx to plot different images from the training set to get #
# a feel for the different kinds of images in the dataset. #
# #
###------------------------------------------------------------------------####
image_idx = 1 #image to plot
cmap = sns.color_palette("Blues", as_cmap=True) #better colourmap from seaborn
pl.figure(figsize = (5,4))
pl.imshow(train_images[image_idx],cmap = cmap)
pl.colorbar()
pl.grid(False)
pl.show()
print('label:', train_labels[image_idx])
label: 0
print('Min: ', np.min(train_images[image_idx]))
print('Max: ', np.max(train_images[image_idx]))
print('Ylabels: ', np.unique(train_labels))
Min: 0 Max: 255 Ylabels: [0 1 2 3 4 5 6 7 8 9]
After playing around with the dataset we notice two things. The first is that the images have a flux/brightness range of 0 - 255. For optimal weight training, we need our dataset to be normalised (sometimes even standardised, depending on what you're trying to do). Normalisation is the process by which you rescale your dataset to be within the range [0,1]. With standardisation, you rescale your dataset to have unit variance and zero mean2.a. For our dataset normalisation should be enough 2.b. So let's do that now2.c:
2a For more see: www.towardsdatascience.com/normalization-vs-standardization-quantitative-analysis-a91e8a79cebf
2b Try implimenting standardisation and see how it would effect the results.
2c Remember that everything you do to the training set, you must also do to the test set.
train_images = train_images/255.
test_images = test_images/255.
print('Min: ', np.min(train_images[image_idx]))
print('Max: ', np.max(train_images[image_idx]))
Min: 0.0 Max: 1.0
The second thing we notice is that the labels range from 0 - 9. We are trying to classify each of the images into one of these types. However, having the labels in this form will not work for the easy model we will be using. We need our labels to be a binary vector. The most common way to change categorical labels into binary vector labels is called One-Hot Encoding3. Our data has 10 categories, therefore we can represent it as a 10 digit binary label, with all digits except for one being 0. Let's have a look at some examples:
3 For more on One-Hot Encoding see: https://towardsdatascience.com/how-and-why-performing-one-hot-encoding-in-your-data-science-project-a1500ec72d85
###------------------------------------------------------------------------####
# Hands on 2 #
# ------------ #
# Change 'label' to different numbers to see their associated OHE #
# representations. #
# #
###------------------------------------------------------------------------####
label = 7 #change this number to see different binary representations
num_classes = 10
print('Label: ',label)
print('Binary: ',tf.keras.utils.to_categorical(label, num_classes))
Label: 7 Binary: [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
# convert class vectors to binary class matrices - this is for use in the categorical_crossentropy loss
train_labels = tf.keras.utils.to_categorical(y_train, num_classes)
test_labels = tf.keras.utils.to_categorical(y_test, num_classes)
# reshape the data into a 4D tensor - (sample_number, x_img_size, y_img_size, num_channels)
# because the MNIST is greyscale, we only have a single channel - RGB colour images would have
image_shape = train_images[0].shape
train_images = train_images.reshape(len(train_images), image_shape[0], image_shape[1], 1)
test_images = test_images.reshape(len(test_images), image_shape[0], image_shape[1], 1)
Our first network ¶
Now we have everything we need to move on to building the network. Tensorflow makes this really easy and intuitive. To build a network, we only need to know what our architecture is going to be. Then we can add each layer line by line. An example of this is shown below.
def make_model_simple(num_classes,input_shape):
'''
Creates a CNN with the specified architecture.
Params:
-------
num_classes: int
The number of classes in the dataset.
input_shape: array
The dimensions of the input images.
Returns:
--------
Tensorflow sequential model.
'''
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(8, kernel_size=(16, 16), strides=(1, 1),
activation='relu',
input_shape=input_shape))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(num_classes, activation='softmax'))
return model
Let's go through this line by line. The first line initiates a tensorflow neural network. In the second line we add the first layer of the network. This first layer is a convolutional layer4. This layer performs the mathematical operation of convolution5 on the input layer and filter. To help with the explaination an illustration of the process is shown below:
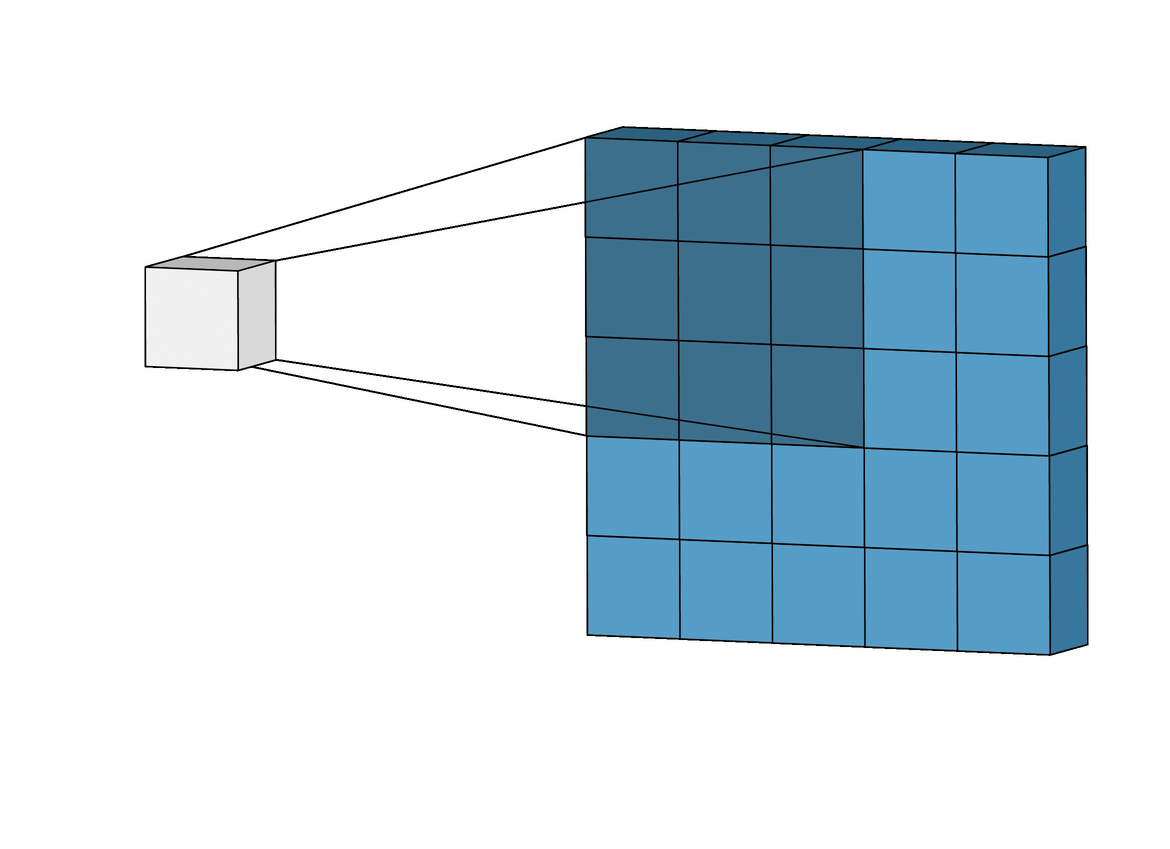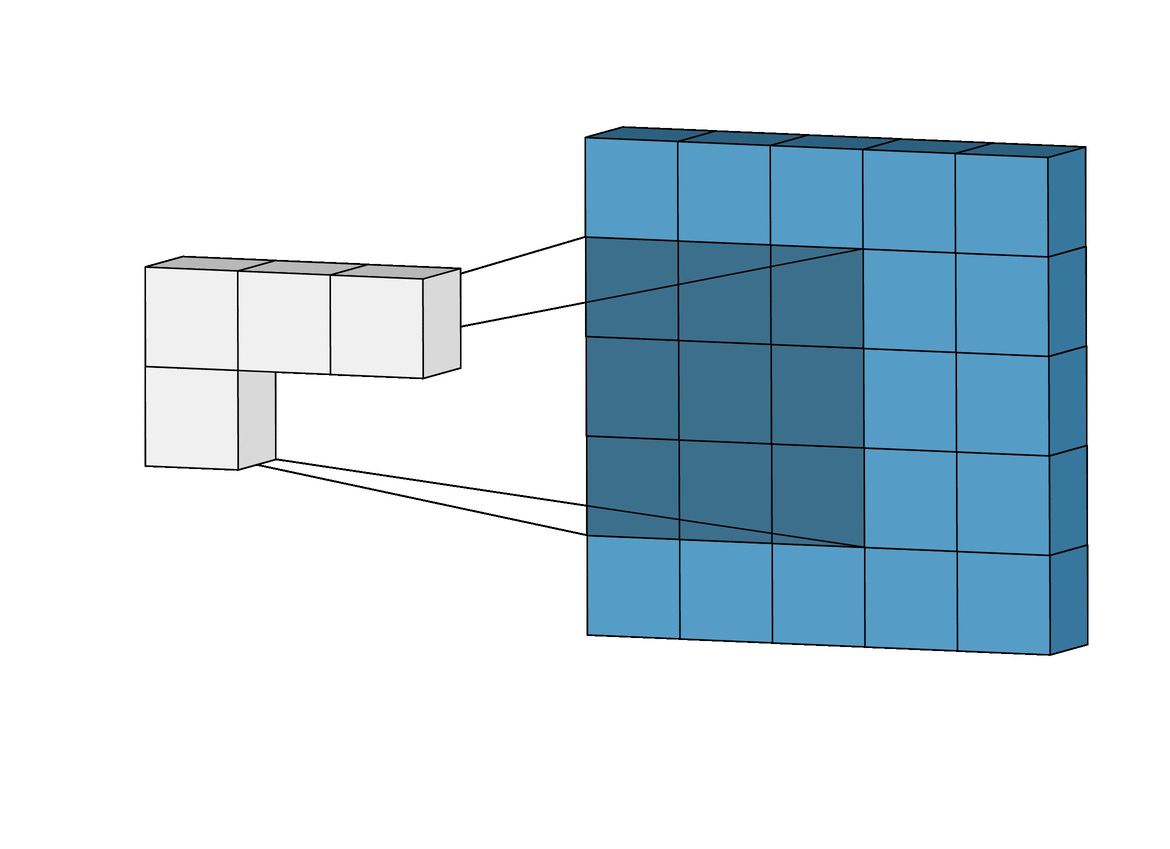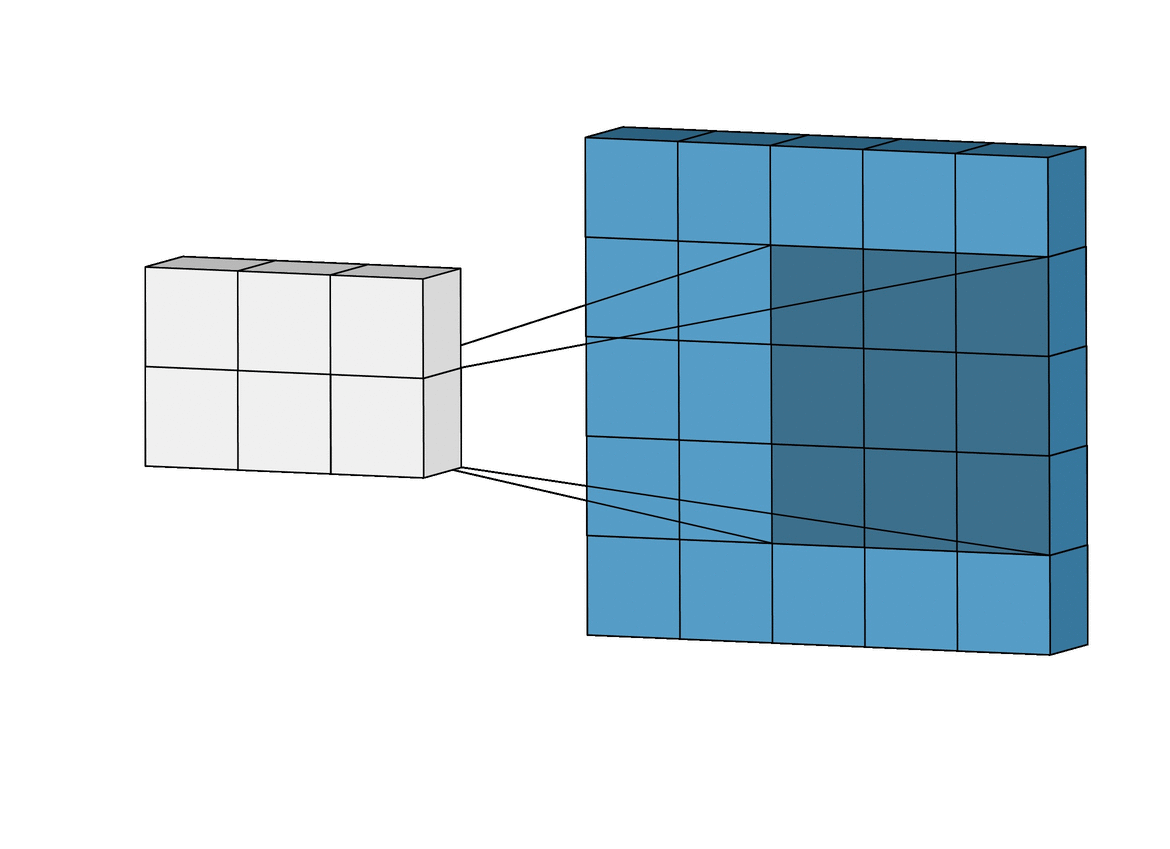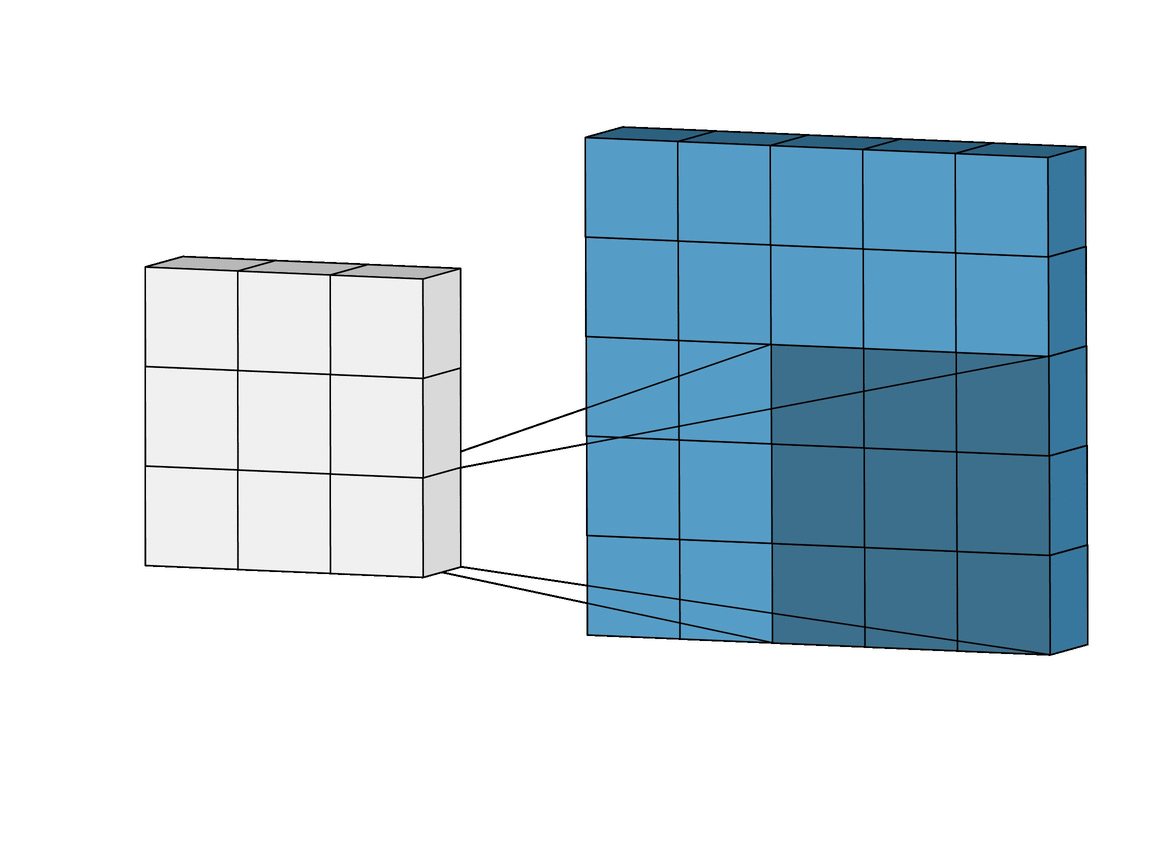
Here we have a 5X5 input image shown in blue and a 3X3 kernel shown in shaded grey. The convolution operation starts with the kernel in the top left corner of the input image, it then performs a matrix multiplication operation between the kernel and the part of the image thats underneath it. The result of this is the first pixel of the output image. The kernel is then slid across the image and this is repeated until you reach the top right corner, the kernel is then moved down and back to the left most pixel. This whole process is repeated building the output image pixel by pixel. The output image is shown being built pixel by pixel in white.
There are 3 important parameters to consider in convolution layers. The first is the number of filters (this is another name for kernels) to use, in our case we have chosen 32. The second is the kernel size, this is the dimension of the kernel, in our case this is 5X5 (in the illustration this is 3X3). The final parameter is strides, this determines the 'sliding' action of the kernel. In the illustration the kernel slides right one pixel until it gets to the end, then slides on pixel down. This means it has a stride of (1,1), which also happens to be the stride of our convolutional layer.
4 For more on CNNs and convolutional layers, see this blog post www.machinelearningmastery.com/convolutional-layers-for-deep-learning-neural-networks/
5 For more on the convolutional operation, see this great video explaination by 3Blue1Brown: www.youtube.com/watch?v=KuXjwB4LzSA
After that really long aside, we can now move on to describing the rest of the network. The second layer is a flatten layer. This layer works much the same way as the flatten operation in Python, it converts the multidimentional output of the convolutional layer into a 1-D array.
The final layer of our network is a Dense layer. These are standard neural network layers, which is just a layer of fully connected neurons. The important parameter in these layers is the number of neurons, which in our case is the number of catagories in our dataset.
#Calls the function and makes a model
model = make_model_simple(num_classes,train_images[0].shape)
#Compiles the network into a graph
model.compile(loss=tf.keras.losses.categorical_crossentropy,
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
2023-07-04 19:38:47.358795: E tensorflow/compiler/xla/stream_executor/cuda/cuda_driver.cc:266] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
In the last line we have introduced a few different concepts, let's go through them one by one. First let's talk about the function model.compile()6. This function compiles our network architecture with the neccessary loss function and optimiser into a computational graph. This is a directional graph that expresses mathematical expressions. Computational graphs underpin all neural networks and is what allows forward and back-propagation to work 7.
The loss function, also known as a cost function or objective function, is used to quantify how well our machine learning model is performing on a given task. The primary goal of the model is to minimise this loss function during the training process. The choice of loss function depends on what you are trying to do and the nature of the data being analysed8. Selecting an appropriate loss function is essential for training a model effectively. In our case we are working with a multi-class classification problem, hence have chosen to use a categorical cross-entropy loss function.
Optimizers are algorithms or methods used to update the parameters of a model during the training process in order to minimise the chosen loss function, thereby improving the model's performance on a given task. The most suitable optimizer depends on the specific task, the architecture of the model, and the size of the dataset. The most common multi-purpose optimizer is called Adaptive Moment Estimation (Adam) and is the one we choose to use here9.
6 www.tensorflow.org/api_docs/python/tf/keras/Model
7 For more on computational graphs and its relation to ML see: www.towardsdatascience.com/evolution-of-graph-computation-and-machine-learning-3211e8682c83#
8 For more on the pros and cons of different loss functions see: www.towardsdatascience.com/loss-functions-in-machine-learning-9977e810ac02
9 For more on optimizers see this great blog post: www.analyticsvidhya.com/blog/2021/10/a-comprehensive-guide-on-deep-learning-optimizers/
Okay, with that all out of the way are we ready to finally train some models? Well not quite yet, we need to introduce two parameters that are fundamental to training a model, namely batches and epochs.
In the previous section we went through loss functions and optimizers. Models train by calculating the loss for a given dataset and then use the optimizer to find a better set of parameters. Now, depending on the dataset, we will not be able to load the entire dataset into memory to calculate the loss10. Instead, the dataset is split into a number of batches. The loss is then calculated for each batch of data and then optimised. One pass through all the batches in a dataset is called an epoch.
With these definitions we can finally train our first model!
10 For more on when and why to use batches see: https://medium.com/analytics-vidhya/when-and-why-are-batches-used-in-machine-learning-acda4eb00763
batch_size = 256 #Number of datapoints in one batch
epochs = 5 #Total number of training passes through the dataset
model.fit(train_images, train_labels,
batch_size=batch_size,
epochs=epochs,
verbose=1)
Epoch 1/5
2023-07-04 19:39:31.144759: W tensorflow/tsl/framework/cpu_allocator_impl.cc:83] Allocation of 188160000 exceeds 10% of free system memory.
235/235 [==============================] - 4s 14ms/step - loss: 0.4910 - accuracy: 0.8630 Epoch 2/5 235/235 [==============================] - 3s 14ms/step - loss: 0.2161 - accuracy: 0.9378 Epoch 3/5 235/235 [==============================] - 3s 14ms/step - loss: 0.1448 - accuracy: 0.9586 Epoch 4/5 235/235 [==============================] - 3s 14ms/step - loss: 0.1125 - accuracy: 0.9661 Epoch 5/5 235/235 [==============================] - 3s 14ms/step - loss: 0.0933 - accuracy: 0.9731
<keras.callbacks.History at 0x7fe63065be50>
#Evaluate the model using the metric chosen above, which was accuracy.
predictions = model.evaluate(test_images,test_labels)
print('')
print('###--------------------------###')
print('### Simple Model ###')
print('###--------------------------###')
print(' Loss: {} '.format(np.round(predictions[0],4)))
print(' Accuracy: {}%\n\n'.format(np.round(predictions[1]*100,2)))
313/313 [==============================] - 0s 924us/step - loss: 0.0860 - accuracy: 0.9739
###--------------------------###
### Simple Model ###
###--------------------------###
Loss: 0.086
Accuracy: 97.39%
Exercise ¶
Okay, even with this super simple model we get pretty good results. But this is to be expected given the easy dataset we have. We could make the results a lot better by adding a few more layers. One has been added for you already. This is a max pooling layer11. See how you can change the preformance of the network by adding different combinations of the four layers you have been introduced to in this tutorial. To get some intiution for what adding more layers and neurons does to the performance of a network play around with this visual toy model provided by tensorflow https://playground.tensorflow.org/.
11 For more on pooling see: www.machinelearningmastery.com/pooling-layers-for-convolutional-neural-networks/
def make_model_intermediate(num_classes,input_shape):
'''
Creates a CNN with the specified architecture.
Params:
-------
num_classes: int
The number of classes in the dataset.
input_shape: array
The dimensions of the input images.
Returns:
--------
Tensorflow sequential model.
'''
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(16, kernel_size=(5, 5), strides=(1, 1),
activation='relu',
input_shape=input_shape))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
####------------------------------------------------------------------####
# #
# #
# #
# #
# Add more layers here #
# #
# #
# #
####------------------------------------------------------------------####
model.add(tf.keras.layers.Dense(num_classes, activation='softmax'))
return model
#This will not run if you didn't add anything to the previous cell. Hint: look at the shapes in the error message, what's wrong here?
model_inter = make_model_intermediate(num_classes,train_images[0].shape)
model_inter.compile(loss=tf.keras.losses.categorical_crossentropy,
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
#Have a play around with the batch sizes and epochs and see what effect they have.
batch_size = 256
epochs = 5
model_inter.fit(train_images, train_labels,
batch_size=batch_size,
epochs=epochs,
verbose=1)
#Evaluate the model using the metric chosen above, which was accuracy.
predictions = model_inter.evaluate(test_images,test_labels)
print('')
print('###--------------------------------###')
print('### Intermediate Model ###')
print('###--------------------------------###')
print(' Loss: {} '.format(np.round(predictions[0],4)))
print(' Accuracy: {}%\n\n'.format(np.round(predictions[1]*100,2)))
Stepping things up ¶
The final network we will be introducing here follows the VGG12 network architecture. This is currently the state-of-the-art architecture in image classification. This is of course overkill for our current toy problem, but it is a very powerful architecture that will be useful for the science case that we will be going through in the next section. This is quite a step up from the other architectures we have used so far, so take your time to have a look at the different layers in the network and use all the resources presented in this notebook to help you understand what each of them do.
def make_model_VGG(output = 1, l_rate = 0.01,loss = 'mean_squared_error',):
'''
Creates a CNN with the VGG architecture.
Params:
-------
output: int
The number of output neurons.
l_rate: float
The learning rate for the given loss function.
loss: str
Loss function to use, only excepts tf loss functions
Returns:
--------
Tensorflow sequential model.
'''
initializer = tf.keras.initializers.GlorotNormal()
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(32, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.Conv2D(32, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
model.add(tf.keras.layers.Conv2D(64, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.Conv2D(64, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
model.add(tf.keras.layers.Conv2D(128, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.Conv2D(128, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
model.add(tf.keras.layers.Conv2D(256, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.Conv2D(256, kernel_size=(3, 3), strides=(1, 1),padding ='same',kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(1024,kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.Dense(1024,kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.Dense(1024,kernel_initializer=initializer,use_bias =False))
model.add(tf.keras.layers.BatchNormalization(beta_initializer=initializer,momentum = 0.9))
model.add(tf.keras.layers.Activation('relu'))
model.add(tf.keras.layers.Dense(output,kernel_initializer=initializer,use_bias =False))
model.compile(loss=loss,
optimizer=tf.keras.optimizers.Adam(learning_rate = l_rate),
metrics=[tf.keras.metrics.RootMeanSquaredError()])
return model